Economía, teoría y práctica

n59, julio-diciembre 2023 | Artículos

DOI: http://dx.doi.org/10.24275/etypuam/ne/592023/Larrosa

Costos acumulativos en expansión de redes con información imperfecta

Cumulative Costs in the Network Expansion with Imperfect Information

Juan Larrosa[*] [0000-0002-0102-9994]

[*] Universidad Nacional del Sur, Argentina. jlarrosa@uns.edu.ar

Resumen

En este artículo se analiza la manera en que se forman las redes en un modelo de información y monitoreo imperfecto en un ambiente de costos de conexión acumulativos. Cada agente sólo observa un número limitado de agentes y debe decidir sus decisiones de conexión óptimas. La estructura óptima de conexiones depende de hasta qué punto el agente puede visualizar el tamaño de la red.

Palabras clave: Juegos no cooperativos, flujo de externalidad bidireccional, estrategias de formación de red, información imperfecta.

JEL: C70, D43, L13.

Abstract

We study the way in which networks are formed in a model of imperfect information and monitoring in a cumulative connection cost environment. Each agent only observes a limited number of agents and must decide its optimal connection decisions. The optimal connection structure depends on the extent to which the agent can visualize the size of the network.

Keywords: Noncooperative games, two-way externality flow, network formation strategies, imperfect information

JEL: C70, D43, L13.

Introducción

Las redes que representan equilibrios de Nash se sustentan en el supuesto de observación perfecta: cada jugador observa a todos los otros jugadores y con quienes deciden conectarse o no, en cada momento del juego.¹ Sin embargo, en muchas ocasiones estas situaciones distan de ser representativas de la situación a modelar. Por ejemplo, puede ocurrir que A conozca a B, B sea visitador frecuente de su primo C y D sea, a su vez, amigo de C. Si D da una información a C, con el tiempo A se terminará enterando dado este esquema de conexiones. Pero, aunque A sepa que C conoce a D puede que A no conozca exactamente toda la información disponible por D que pueda ser de su beneficio, cuestión que C, quien mantiene un lazo directo con D, podría sí saber. Eso se solucionaría si A también estableciese un enlace directo con D. Cuando sucede esto podemos decir, en términos de teoría de juegos, que A monitorea imperfectamente la estructura de conexión de C y que tiene información imperfecta acerca del valor de la información de D. Las redes creadas en ambientes de monitoreo e información imperfecta generan, usualmente, estructuras de equilibrio diferentes a las emergentes en caso de monitoreo perfecto e información perfecta. McBride (2006, 2008) lo prueba partiendo de los aportes de juegos de formación de redes de Bala y Goyal (2000) y el esquema formal de equilibrios de información imperfecta de Gilli (1999). En este trabajo me propongo aplicar el esquema de información imperfecta postulado por los aportes de McBride (2006, 2008) junto con McBride y Hewitt (2013) y Nava y Piccione (2014) para el caso de considerar costos acumulativos en la conexión de los agentes. ¿Por qué considerar costos acumulativos?

Existen varios ejemplos modernos e históricos de presencia de costos acumulativos en la creación de redes, aunque recurrentemente asociados a infraestructura. Por ejemplo, los costos acumulativos se analizan modernamente en Chinowsky, Price y Neumann (2013) desde el punto de vista ambiental en donde la erosión debido al incremento de la temperatura desgasta el pavimento. Ello genera costos acumulativos de adaptación al nuevo marco climático que asciende a miles de millones de dólares en infraestructura. En un contexto más histórico, la creación de las rutas romanas o vías ha sido estudiada muchas veces en un esquema de costos acumulativos. Shipley (1931) ilustra detalladamente cómo cada tipo de inversión en infraestructura de caminos produjo grandes debates y quejas por los costos incrementales de la extensión de las obras, es decir un costo acumulativo en infraestructura. Pero también Laurence (1998: 129) ejemplifica el costo creciente de transporte por medio de bueyes en las rutas del imperio aumentando incluso un 40 por ciento al superar las 100 millas romanas, es decir un costo acumulativo de transporte. En Roma extender una red afectaba tanto a quienes las construían como a quienes las operaban. Este mismo ejemplo histórico revela también un aditamento: muchas regiones del imperio eran poco conocidas y menos aún observadas regularmente por las autoridades romanas. Las Galias, Britania, Germania, entre otras, eran provincias conflictivas, con frecuentes rebeliones y con muchos lugares de difícil acceso. En este marco particular, las redes de caminos (enlaces) unen puntos geográficos específicos (nodos) de una red con costos acumulativos de construcción y operación en la cual, sobre todo, los nodos potenciales de expansión se carece de información perfecta. ¿Cuál sería la estructura de conexión óptima para estos casos? ¿Conviene sostener la expansión de una red no conociendo ex ante todos los posibles nodos desde una base o punto de inicial?

Este trabajo inicia con la reproducción de algunos resultados necesarios de aportes citados en el contexto de información perfecta y añade como aporte original la adaptación de dichos teoremas al contexto de información o monitoreo imperfectos con costos acumulativos con redes no dirigidas (proposiciones 5 y 7), ítems tampoco analizados por las contribuciones citadas. Se encuentra que el grado de observación que posee un agente afecta la topología óptima. A medida que el grado de observación se va incrementando, el resultado de equilibrio converge al resultado de información y monitoreo perfectos, es decir, una red de línea con nodos activos pares o impares, resultado deducido en una contribución previa (Larrosa y Tohmé, 2006). Es un resultado razonable y observable si nos atenemos al supuesto que los costos se van acumulando a medida que extendemos el sendero. Sin embargo, con baja observación, las redes tienen a comprimirse de manera ineficiente.

A continuación, desarrollamos el modelo. La sección I plantea las definiciones iniciales de un juego de formación de redes no cooperativo, la sección II presenta el equilibrio con monitoreo perfecto mientras que la sección III hace lo propio con el caso de modelo imperfecto. La siguiente sección finaliza con las conclusiones.

I. El Modelo

Sea N = (1,…, n) un conjunto de agentes. Para evitar resultados triviales siempre vamos a suponer que 3≤ n < ∞. Se supone que cada agente i ϵ N posee una información que todos los otros individuos desean conocer. El modelo trabaja con grafos no dirigidos. A continuación, se definen conceptos y herramientas comunes al desarrollo de toda la argumentación del presente trabajo.

Sea N = (1,…, n) un conjunto de agentes. Para evitar resultados triviales siempre vamos a suponer que n ≥ 3. Si i y j son dos miembros típicos de N, un enlace entre ellos, sin intermediarios, originado en i y finalizado en j será representado como ij. La interpretación de ij es que i establece un contacto con j que permite a i tener acceso a la información de j, así como a su red de contactos.

Cada agente i ϵ N tiene alguna información de su propiedad, v_i ϵ Z₊ (es decir, representado como un entero positivo). Por convención inicialmente supondremos que la información de cada agente es lo suficientemente valiosa como para que valga la pena establecer un enlace con ella,² es decir que v_i > 1. Como se mencionó i puede acceder a más información formando enlaces con otros agentes. Los agentes tratarán de maximizar la utilidad de la información disponible para ellos, así como minimizar el costo de conexión con otros agentes. Para lograr ello, ellos estarán dotados con un conjunto de estrategias. Cada estrategia para i ϵ N es un vector $g_{i} = 〈g_{i, 1}, \dots, g_{i, i - 1}, g_{i, i + 1}, \dots, g_{i, n}〉$ de (n - 1) dimensiones donde cada g_i,j para j ≠ i vale 0 o 1. Esto es interpretado como significando que i establece un enlace directo con j si g_i,j = 1 mientras que si g_i,j = 0 dicho enlace no existe. El conjunto de todas las estrategias se anota como G_i. Restringimos nuestro análisis sólo a los casos de estrategias puras, lo cual implica que |G_i | = 2^n-1. Finalmente, G = G₁ ×…× G_n denota el conjunto de perfiles de estrategia en la interacción entre los agentes de N.

Decimos que existe un sendero desde j hacia i de acuerdo al g ϵ G si existe una secuencia de agentes diferentes (para evitar que existan ciclos) j₀,…, j_m (con i = j₀ y j = j_m) tal que g_{j0, j1} = … = g_{jm-1, jm} = 1. En palabras, dada una estrategia conjunta g, tenemos que $j_{1} {\in_{g} N}^{g j 0}, j_{2} \in N^{g j 1}, \dots, j_{m} \in N^{g j m - 1}$ . Un sendero desde j = j_m hacia i = j₀, denotada como j (i, tiene una longitud, la cardinalidad de la secuencia j₁ , j₂ ,…, j_m-1 , j_m, es decir m, el cual indica el número de enlaces intermedios entre j e i. Nótese que un enlace dirigido es un sendero de longitud 1.

Pasemos a continuación a analizar el caso en que la información fluye en dos direcciones una vez establecido el contacto. Cada jugador i elige con quien iniciar un enlace de comunicación costoso. Sea la estrategia del jugador i definida por g_i = (g_i,1 ,…, g_i,i-1, g_i,i+1 ,…, g_i,n) donde g_i,j = 1 significa que i ha iniciado un enlace a j y g_i,j = 0 significa que i no ha iniciado un enlace con j. Definimos entonces a G_i como el conjunto de perfiles de posibles enlaces de i y notemos a G = G₁ × … × G_n.

El perfil de estrategias de los jugadores g = (g₁,…, g_n) G puede ser representado por un grafo o estructura de red en la cual los jugadores individuales pueden ser representados por nodos y los enlaces que ellos establecen entre sí por líneas o flechas. El jugador i conoce la información de j porque existe un sendero entre ellos. Formalmente, existe un sendero en i y j si alguno de los siguientes es verdadero:

(i) m á x \{g_{i, j}, g_{j, i}\} = 1 (c o m u n i c a c i ó n d i r e c t a)

(i i) e x i s t e n j u g a d o r e s j_{1}, \dots, j_{m} d i s t i n t o s e n t r e s í y d i s t i n t o d e i y j t a l q u e m a x

\{g_{i, j 1}, g_{j 1, i}\} = m á x \{g_{j 1, j 2}, g_{j 2, j 1}\} = m á x \{g_{j m, j}, g_{j, j m}\} (c o m u n i c a c i ó n i n d i r e c t a)

Si bien la información fluye hacia ambos lados a través de un enlace (comunicación bidireccional), estos grafos son dirigidos porque toman en cuenta el costo de iniciación del enlace (g_i,j = 1 implica que i financia el enlace y, por lo tanto, no tiene la misma interpretación que g_j,i = 1 tal como lo requiere la definición de grafo no dirigido).

Un componente es un subconjunto de la red tal que existe un sendero entre dos jugadores en el componente y no existe ningún sendero entre cualquier jugador en el componente y cualquier jugador fuera del componente. Sea N_i ⊆ N la forma de denotar el conjunto de jugadores dentro del componente de i y sea n_i el número de jugadores en dicho conjunto. Sea I_i ={j ϵ N | j ≠ i, s_ij = 1} el conjunto de individuos con quienes i inicia un enlace y también el número de individuos en ese conjunto.

Una red se dice conectada si soporta un único componente. Sí ese único componente es mínimo g se dice mínimamente conectada. Una red no conectada se dice desconectada. Una instancia particular de las redes mínimamente conectadas es la red de estrella centralmente sostenida, g^s de ahora en más, la cual requiere que el agente i tenga conexiones con todos y los otros agentes no tengan ninguna conexión. Así, los agentes pueden ser etiquetados (por medio de una función l : N → N) como {l(1),…, l(n)} y sus estrategias serían g_l(1),l(2) = g_l(1),l(3) =…= g_l(1),l(n) = 1 y no hay otros enlaces (ver Figura 1). Otra instancia es la red de línea, g^l de ahora en más, en la cual las estrategias de conexión son: g_l(1),l(2) = g_l(2),l(2) = … = g_l(n-1),l(n) = 1 y no hay otros enlaces. Dado que el flujo es bidireccional puede ocurrir que dentro de la red de línea los agentes inicien las conexiones de muchas diferentes maneras y aún así permitan el flujo de información a lo largo de la misma. Es decir, dentro de la red de línea existen distintos grafos de activación de la conexión secuencial que otorgan pagos diferentes a los agentes. La red de línea con nodos de activación ordenados mantiene una configuración de conexiones que hacen que el primero se conecte con el segundo, el segundo con el tercero y así hasta completar la secuencia siendo el antepenúltimo que se conecta con el último y no hay más conexiones.

Figura 1

Red de estrella centralmente sostenida.

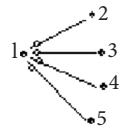
Fuente: Elaboración propia.

Se pueden destacar algunas formas de activación de la red de línea. Por ejemplo, configuraciones alternativas red de línea con nodos activos impares, g^li, es una topología lineal que puede ser representada por

g_{l (1), l (2)} = g_{l (3), l (2)} = g_{l (3), l (4)} = \dots = g_{l (n - 3), l (n - 4)} = g_{l (n - 3), l (n - 2)} = \dots = \{\begin{matrix} g_{l (n - 1), l (n)} = 1 s i n e s p a r \\ g_{l (n), l (n - 1)} = 1 s i n e s i m p a r \end{matrix}

es decir los nodos impares inician un enlace con sus predecesores y sucesores inmediatos, mientras que los pares pasivamente aceptan hasta completar la secuencia de conexión. Finalmente, una estructura análoga es la red de línea con nodos activos pares, g^lp, que es aquella que cumple con la configuración

g_{l (2), l (1)} = g_{l (2), l (3)} = g_{l (4), l (3)} = \dots = g_{l (n - 3), l (n - 2)} = g_{l (n - 1), l (n - 2)} = \dots = \{\begin{matrix} g_{l (n), l (n - 1)} = 1 s i n e s p a r \\ g_{l (n - 1), l (n)} = 1 s i n e s i m p a r \end{matrix}

es decir que los nodos etiquetados como pares inician las conexiones hacia sus nodos inmediatamente vecinos mientras que el resto de nodos actúan pasivamente (no inician ellos la conexión). La Figura 2 muestra un ejemplo de cinco agentes para cada uno de los casos descriptos en esta sección.

Figura 2

Diferentes formas de activación de redes de línea de conexión secuencial.

Fuente: Elaboración propia.

La función de utilidad de la agente está sostenida en la cantidad de información a la que accede y en los costos de dicho acceso. Cada agente i ϵ N tiene alguna información de su propiedad, v_i ϵ Z₊ (es decir, representado como un entero positivo). Por convención, inicialmente supondremos que la información de cada agente es lo suficientemente valiosa como para que valga la pena establecer un enlace con ella,³ es decir que v_i > 1. Sea ni(g) el conjunto y número de individuos con quienes i ha iniciado un enlace según la estrategia g. Así, el valor de la información total accedida por la agente i, I_i, queda definido por:

(1)

I_{i} (g) = v_{i} + Σ_{j \neq i |j \in N} I_{j} (n_{i} (g))

donde v_j es el valor de la información del agente j (exógeno al agente i), n_i (g) representa el conjunto de agentes accedidos (la estructura de conexión) del agente i según su perfil de estrategias g. La función mantiene una forma genérica para que pueda ajustarse a casos concretos.

Supondremos u_i: G → R a la función de utilidad para el agente i, que será formalizada como:

(2)

u_{i} (g) \equiv I_{i} (g) - c \sum_{j \in N^{i; g}} μ_{i} (g)

donde I_i representa la información poseída y accedida por el agente i según la estrategia de conexiones g de la definición (1), c representa el costo de cada conexión, que para nuestro caso particular suponemos como c = 1 y la función de costos se define como:

(3)

μ_{i} (g) = \sum_{j \in N^{i; g}} μ_{j} (g) + \sum_{k \in N^{j; g}} μ_{k} (g), \forall i, j, k \in N |k \neq i \neq j

Aquí queda también discriminado el grado de cercanía de los enlaces. El primer término de (3) se corresponde a los enlaces directos del agente i mientras que el segundo término refiere a los enlaces indirectos del agente, los cuales también tiene que solventar. Esto es, los pagos de i son la suma de toda la información que puede ser accedida por ella, menos el costo de los senderos (es decir conexiones directas e indirectas) que llegan a ella, que están establecidos de acuerdo a g (recuérdese que cada enlace se supone tiene costo unitario). La intuición aquí es que i obtiene un pago por acceder a mayor información, pero al mismo tiempo ella tiene que pagar un cargo o arancel por cada uno de los enlaces en los senderos hacia las fuentes de información. Debe destacarse que los costos no decaen con las distancias, sino que se mantienen constantes generando un proceso acumulativo de los mismos.

Otros supuestos del modelo son:

El valor v_i no cambia a medida que más jugadores conozcan dicha información;
El valor de v_i no cambia a medida que un individuo en particular conozca más información, y
Las informaciones son transmitidas claramente a través de la red (no hay distorsión de información ni decaimiento de flujo) tal que el valor de v_i para j es el mismo sea que i y j estén conectados directa o indirectamente.

Iniciemos a continuación la investigación recordando los resultados de un modelo con monitoreo perfecto.

II. Monitoreo perfecto

El monitoreo perfecto, también denominado perfecta observación, implica que, luego que los jugadores simultáneamente toman sus decisiones de enlaces, cada jugador observa la estructura de red resultante. La red resultante g* es un equilibrio si, después de observar g*, ninguna jugadora i conoce una desviación de g* que la deje a ella en un nivel de utilidad estrictamente mejor. Este supuesto es la base de una red de Nash tal como fue postulada por Bala y Goyal (2000) y adoptada por este autor en otras contribuciones (Larrosa, 2005). Partamos de unas definiciones básicas:

Definición 1: Un equilibrio de Nash (puro) del juego (G_i , u_i)_iϵN es un perfil de estrategias {g*}_iϵN tal que para cada iϵN, , $g_{i}^{*}, (g_{- i}^{*}) \geq u_{i} (g_{i}, g_{- i}^{*}), {\forall g}_{i}^{'} \in G_{i}$ .

Una red de equilibrio bajo monitoreo perfecto es entonces un equilibrio de Nash (o red de Nash). Con esto establecido, tenemos que:

Proposición 1: Bajo perfecto monitoreo una red de equilibrio debe ser mínimamente conectada y cualquier red mínimamente conectada es un equilibrio. Más aún, una red es eficiente si y sólo si es mínimamente conectada. (Bala y Goyal, 2000: 1194).

Se remite a las referencias puntuales para las pruebas, pero básicamente la Proposición 1 elimina todos los enlaces redundantes y hace que la información dentro de la red fluya de la manera más eficiente posible. El criterio de eficiencia está asociado a que la información recorra la red en la menor cantidad de pasos posibles. Aquí existe un problema de coordinación extremadamente difícil de garantizar en un juego de movidas simultáneas. Bala y Goyal (2000) describen una dinámica simple a través de la cual las acciones de los agentes (en un esquema de juegos repetidos) harán converger a redes mínimamente conectadas sin ninguna coordinación formal.

Ahora continuamos con el desarrollo de McBride (2006) sobre la información imperfecta en juegos de formación de red.

III. Monitoreo imperfecto

La posibilidad de existencia de monitoreo imperfecto requiere que se expliciten algunas condiciones iniciales. Se adoptará el criterio de McBride (2006) en el cual los agentes observan todos los enlaces dentro de la distancia geodésica x, x ³ 1, para luego variar x para observar cómo esos cambios afectan los resultados de equilibrio.

Veamos por ejemplo la Figura 3(a). En ella vemos al agente 1 cuando su capacidad de observación es de sólo un enlace de distancia (x = 1). Aquí, sólo el agente 2 es observable para 1. En cambio, en 3(b) vemos que cuando x = 2 ya el agente 1 accede a la información y monitoreo de los agentes 5 y 3. Ya con x = 3 (Figura 3(c)) el agente 1 logra observar toda la red. Como se aprecia, con niveles bajos de x un agente no puede aprovechar totalmente el potencial que le brinda la asociación con agentes de su entorno. A medida que x crece el agente puede acceder a niveles de utilidad mayores dado que acceder a información, según la presente modelización, siempre resulta en incrementos netos en el bienestar individual.

Figura 3

Ejemplos de distintos conjuntos de información según x.

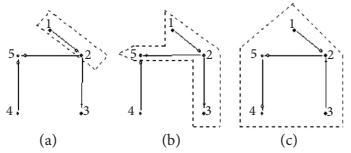
Fuente: Elaboración propia.

Este esquema de monitoreo imperfecto denominado observación de x enlaces, intenta replicar situaciones observadas en la realidad. Los modelos de difusión en redes estimados a través de datos empíricos revelan que los individuos son afectados en mayor cantidad de veces y con mayor intensidad por los lazos directos que por aquellos indirectos (Bondonio, 1998). Esto puede ser visto como algo más intuitivo: podemos observar las relaciones que establecemos con nuestros allegados más cercanos, pero se hace más difícil saber cuando estas interacciones se refieren a enlaces cada vez más lejanos.

La segunda pregunta devenida de la falta de observación es: ¿cuál es el concepto de equilibrio apropiado para estas situaciones? Un equilibrio de Nash, como el definido anteriormente, supone que todos los agentes tienen información perfecta (incluyendo en este caso observación perfecta también) acerca de las acciones de todos los otros jugadores por lo que dicho concepto no es el apropiado cuando se presenta un caso imperfecto. Siguiendo nuevamente a McBride (2006) vamos a emplear el concepto de equilibrio conjetural que no impone esta restricción (Gilli, 1999). Este concepto esta diseñado para juegos en los que los agentes observan sólo un subconjunto de las acciones de los otros agentes:

Definición 2: Un juego de monitoreo imperfecto es una combinación ${〈G_{i}, u_{i}, m_{i}〉}_{i \in N} [/ p]$

Luego que las acciones han sido elegidas y un g es generado, el jugador i recibe un mensaje (señal) m_i que revela algún subconjunto de g. En general, m_i dependerá de las acciones elegidas, por lo que sea la señal de i una función m_i (g) o m_i (g_i , g_-i).

En un ambiente de monitoreo imperfecto, luego que las elecciones de los jugadores formen un g_i, m_i revela g a cada i, es decir, m_i (g) = g, “i. Con observación de x enlaces, sin embargo, m_i revela a i esa parte de g dentro de los x enlaces de i en el componente i de N_i en ese g. Sea L_i (y) el conjunto de jϵN_i que están exactamente y alejados a lo largo de algún sendero de i hacia j, donde L_i (0) = {i} y L_i (∞) = {j | j $\notin$ N_i}. Ahora se describe formalmente qué quiere decir observación de x enlaces con el siguiente supuesto:

Supuesto: Considérese un juego de red con monitoreo imperfecto caracterizado por observación de x enlaces. Luego que los jugadores hacen sus movidas simultáneas que resultan en g, el mensaje m_i (g) del jugador i es el siguiente:

m_{i} (g) = \{\begin{matrix} g_{j} p a r a t o d o j \in \{L_{i} (0) \cup L_{i} (1) \cup \dots \cup L_{i} (0)\} y \\ g_{k, j} p a r a t o d o k y j t a l q u e k \in L_{i} (x) y j \in L_{i} (x - 1) \end{matrix}\}

La primera línea entre corchetes son todos los enlaces hechos por cualquier jugador a x - 1 enlaces o menor distancia de i. La segunda línea suma aquellos jugadores x enlaces más enlaces más lejanos quienes establecen un enlace con alguien que se encuentra a x - 1 enlaces de i. Nótese que los enlaces iniciados por alguien a x + 1 enlaces no serán observados ni los enlaces iniciados por alguien que esté a x enlaces de distancia hacia otro que este a x + 1 enlaces de éste. Para definir un equilibrio conjetural, sea p_i (g) la distribución de probabilidades sobre todo gϵG e interprétese a p_i como las creencias de i.

Definición 3: Un equilibrio conjetural es un perfil de acciones y creencias ${(g_{i}^{*}, π_{i}^{*})}_{i \in N}$ tal que para cada $i \in N$ :

1. $\sum_{g \in G} π_{i}^{*} (g) u_{i} (g_{i}^{*}, g_{- i}^{*}) \geq \sum_{g \in G} π_{I}^{*} (g) u_{i} (g_{i}^{'}, g_{- i}^{*}), p a r a t o d o g_{i}^{'} \in G_{i};$

2. Para cualquier $g \in G$ con $π_{i}^{*} (g) > 0, d e b e s e r q u e m_{i} (g^{*}) = m_{i} (g)$ .

La condición 1 establece que en equilibrio cada acción del jugador $g_{i}^{*}$ debe ser una mejor respuesta dadas las conjeturas $π_{i}^{*}$ . La condición 2 establece, por su parte, que para cualquier jugador que asigne probabilidades no nulas a cierto estado del mundo g, la señal recibida por ese jugador en ese estado del mundo debe ser igual que la señal del jugador en el verdadero estado del mundo g*. Es decir, las creencias del jugador no deben contradecir la información acerca del estado del mundo en el mensaje del jugador.

Para el juego de red, una combinación ${(g_{i}^{*}, π_{i}^{*})}_{i \in N}$ es un equilibrio si, después de tomar las decisiones de enlaces simultáneamente y después de recibir las señales, ningún jugador tiene incentivos para cambiar sus creencias o acciones. Una restricción adicional sobre los $π_{i}^{*}$ que se realiza es que $π_{i}^{*}$ debe tener en cuenta el conocimiento de un jugador del marco del juego. Esta restricción adherida tiene una implicación inmediata para las creencias de equilibrio de los jugadores.

Postulado 1: Considérese un equilibrio ${(g_{i}^{*}, π_{i}^{*})}_{i \in N}$ donde $n_{i}^{*}$ es el número de jugadores en el componente de i en.g* Para cualquier estado g’ ∈ G tal que $π_{i}^{*} (g^{'}) > 0$ es necesario que el número de jugadores en el componente i en g’ deben también ser igual $n_{i}^{*}$ .

Prueba: Véase McBride (2006: 105).

Si bien no se reproduce la prueba al comentario, sí se puede justificar del siguiente modo. Supongamos un equilibrio ${(g_{i}^{*}, π_{i}^{*})}_{i \in N}$ Luego que se toman las decisiones de conexión y la estructura resultante de dichas decisiones se hace visible, un jugador observa su utilidad ex post $u_{i}^{*} (g) \equiv I_{i} (g^{*}) - c \sum_{j \in N^{i; g}} μ_{i} (g^{*})$ El jugador i conoce v y c dado que se supone que el esquema de juego es comúnmente conocido. Él también conoce I_i dado que es calculado por la suma de sus elecciones de conexión: $I_{i} (g^{*}) = v_{i} + \sum_{j \neq i |j \in N} I_{j} (n_{i} (g))$ Restringiendo sus creencias de equilibrio para contabilizar el conocimiento de $n_{i}^{*}$ se infiere que cualquier g’ que genere $n_{i} \neq n_{i}^{*}$ no debe de ser el verdadero estado de la naturaleza. La restricción sobre $n_{i}^{*}$ . en el Postulado 1 toma en cuenta este conocimiento. Al final, dicho postulado es un equivalente a una noción de equilibrio. Una red de equilibrio debiera ser una en la que un jugador no querrá cambiar su decisión incluso después de la observación ex post de la estructura de enlaces y la revisión ex post de su función de utilidad.

Se sabe que el concepto de equilibrio conjetural potencialmente permite la existencia de muchos posibles equilibrios dado que pone muy pocas restricciones a las creencias. La tercera pregunta que quiere responder McBride entonces es: ¿si un jugador no observa ciertos enlaces de jugadores, entonces qué creencias debiera tener el jugador acerca de esos enlaces? McBride usa aquí la siguiente aproximación: elegir una estructura de red y buscar las creencias que conviertan a esa combinación de acciones y creencias en un equilibrio. Si bien ello da un conjunto grande de potenciales equilibrios, ahorra el incluir supuestos acerca de qué debieran creer los agentes sobre los enlaces que no son observados por ellos. Por ello, la única restricción impuesta a las creencias es que sean consistentes con la información revelada quedando así el equilibrio conjetural como condición necesaria para el equilibrio. Analicemos ahora el equilibrio con observación de x enlaces.

III.1. Equilibrio con observación de x enlaces

Equilibrio conjetural implica que:

Postulado 2: Cualquier equilibrio bajo perfecto monitoreo es también un equilibrio bajo observación de x enlaces para cualquier x. Mas aún, cualquier equilibrio bajo observación de x enlaces, x > 1, es también un equilibrio bajo observación de enlaces para todo x’< x. (McBride, 2006).

Un equilibrio de Nash (EN) es un equilibrio conjetural (EC) con la restricción de que $π_{i}^{*} (g^{*}) = 1, \forall i \in N$ . Dado que la observación de x enlaces impone pocas restricciones sobre las creencias de equilibrio que el EN, las restricciones sobre las creencias en una EN satisfacerán las restricciones más débiles de un EC con un x finito. Las “creencias correctas” en un EN sostendrán una red como equilibrio bajo observación restringida si los jugadores coinciden en creer en las creencias correctas. La segunda parte del Postulado 2 sigue una lógica similar. Si fijamos un x > 1 y x’ < x, entonces la observación de x’ enlaces pone menores restricciones sobre las creencias que lo hace una observación de x enlaces, por lo que incluso creencias incorrectas bajo la más grande observación, de x enlaces, debe aún satisfacer las restricciones más débiles bajo la más pequeña observación, de x’ enlaces.

Algo interesante de este resultado es que las redes eficientes de Nash siguen siendo equilibrios en el caso de monitoreo imperfecto. Desdichadamente no existe una explicación de cómo los jugadores caen en las creencias correctas especialmente cuando cada jugador sólo observa una porción limitada de la red. Ello lleva a creer que los jugadores pueden tener las creencias correctas en equilibrio y que aún así éstas podrían sostener redes ineficientes como equilibrios.

McBride (2006: 107) demuestra posteriormente que la visualización parcial de la red hace que los agentes no puedan determinar si se ha formado un ciclo en la estructura de conexiones establecida por los agentes. Así, se establece que un ciclo de tamaño y será observado si $x \geq \frac{y}{2}$ y un ciclo de tamaño y o mayor no será observado.

Proposición 3: Si $x \geq \frac{n}{2}$ , entonces cualquier red de equilibrio debe ser mínimo, pero si $x < . \frac{n}{2}$ , entonces siempre existen redes de equilibrio con uno o más ciclos de tamaño y = {2x + 1, 2x + 2, … , n}.

Prueba: McBride (2006: 107).

La Figura 4. (a) muestra un equilibrio con un rango de observación de x = 2. La información de 1 no revela al jugador 1 el lazo entre 3 y 4, por lo tanto, no percibe el ciclo. Aquí x es estrictamente menor que $\frac{y}{2} (\frac{5}{2})$ (). Entonces, ningún agente llega a observar el ciclo con este valor de rango de observación y con esta cantidad de agentes. Obsérvese que si x = 3 entonces todos los agentes observarían el ciclo. Si 1 observara el ciclo, asignaría $π_{1}^{*} (g^{'}) = 0$ para cualquier g’ ∈ G que no tenga el ciclo. Nuevamente, el problema del ciclo para las estructuras óptimas de comunicación es la aparición de enlaces redundantes.

Figura 4

Diferentes rangos de observación.

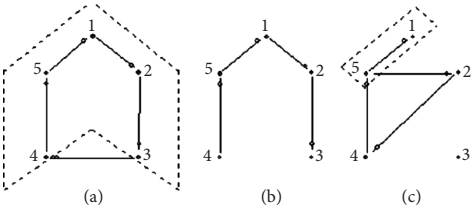
Fuente: Elaboración propia.

Recordemos que, por la definición del modelo, conectarse paga más que desconectarse. Por ello, las ineficiencias más peligrosas pueden aparecer por una falta de conexiones. En el caso de la Figura 4 (c) nos encontramos con un ejemplo peor. Dado que x = 1 para todos los agentes, ninguno puede visualizar a la agente 3, por lo que permanece desconectada del resto en equilibrio. Al haber supuesto que v_i > c, este es uno de los resultados más ineficientes. Verifiquemos bajo qué condiciones estos problemas pueden ser evitados. Para ello, McBride postula la siguiente proposición:

Proposición 4: Si $x > \frac{n - 4}{4}$ , entonces cualquier red de equilibrio es conectada. Sin embargo, si $x < . \frac{n - 4}{4}$ y c es suficientemente alto, entonces existen equilibrios de redes desconectadas y cada jugador en una red desconectada debe estar en un componente con al menos 2x + 2 jugadores.

Prueba: McBride (2006: 108).

En palabras, si definimos a un agente b como el mejor observador de un componente N_i. Sea d^* la distancia entre el agente i y el agente en su componente que es el que está más alejado, j. Entonces b tiene la menor $d_{b}^{*}$ con respecto a cualquier otro agente. Si x³ $d_{b}^{*}$ entonces b observa a todos los agentes y si x < $d_{b}^{*}$ entonces ningún agente observa a todos los demás. En la Figura 4. (b) el agente b es 1 y $d_{b}^{*}$ = 2. Se puede hacer notar que $d_{b}^{*}$ puede ser n_i /2 si cuando n_i es par o (n_i - 1)/2 cuando n_i es impar. Ahora fijemos que cuando n_i es par, $d_{b}^{* 3}$ n_i /2 por lo que x < n_i /2 es una condición necesaria para un equilibrio desconectado, lo que se traduce para un n_i genérico que x < (n_i - 2)/2, lo cual implica que n_i = 2x +2 como una condición necesaria para un equilibrio desconectado.

Teniendo toda esa información, podemos especificar una topología prevaleciente para el caso de una función de costos acumulativos bajo información imperfecta. Tres pasos previos habrá que seguir: primero, es necesario readecuar el supuesto de aversión a la inequidad al esquema de información imperfecta; segundo, se requiere reforzar un concepto de desconexión como comportamiento irracional bajo la estructura de pagos presente, y finalmente, establezcamos en modelo de comparación deducido en Larrosa y Tohmé (2006). Así, se formula la proposición:

Proposición 5: Bajo observación completa y cumpliendo el supuesto de aversión a la inequidad (SAI), el conjunto de redes de equilibrio estrictas de Nash es el conjunto de redes de línea secuenciales de nodos pares activos e inactivos y cada una de esas redes de línea es eficiente.

Prueba: Larrosa (2005).

La segunda proposición nos dice que bajo el esquema de información imperfecta ningún jugador racional va a esperar que otro jugador racional juegue una estrategia de desconexión o aislamiento.

Proposición 6: Cualquier equilibrio racionalizable esta conectado para cualquier x.

Prueba: McBride (2006: 18).

En breve, dado que los jugadores se saben racionales entre sí, ningún jugador asignará una probabilidad positiva en equilibrio a una red en que otro jugador juegue a permanecer aislado.

Seguimos con el último paso previo. Podemos enfocarnos en el caso de observación de x enlaces. Recordando los hallazgos de Berninghaus y otros (2004) y de Falk y Kosfeld (2012) postulamos un refinamiento al modelo de información incompleta bajo análisis que consiste en la adición de un supuesto de conducta. Primero se debe definir el concepto de coeficiente conjetural de asimetría de los beneficios $\hat{ς} (g)$ tal que

(4)

\hat{ς} (g) = \frac{n}{(n - 1) (n - 2)} \sum_{i \in N} {(\frac{\sum_{g \in G} π_{i} (g) u_{i} (g_{i}, g_{- i}) - \sum_{g \in G} π_{i} (g) {\bar{u}}_{i} (g_{i}, g_{- i})}{σ})}^{3}

donde s representa el desvío estándar de los beneficios entre los miembros de dicha red, $\sum_{g \in G} π_{i} (g) u_{i} (.)$ representa la utilidad del agente i dadas las creencias de que la estrategia g será jugada por todos los agentes y $\sum_{g \in G} π_{i} (g) {\bar{u}}_{i} (.)$ representa el beneficio promedio para cada agente que se cree tendrá si todos deciden conectarse bajo el perfil de estrategias g. Dado esto, definimos ahora:

Supuesto de aversión conjetural a la inequidad (SACI). Dadas dos estrategias distintas y conjuntas g y g’ y sea que $\sum_{g \in G} π_{i} (g) u_{i} (g_{i}, g_{- i}) \equiv \sum_{g \in G} π_{i} (g) u_{i} (g_{i}^{'}, g_{- i})$ . Si las creencias deciden que $\sum_{g \in G} π_{i} (g) u_{i} (g_{i}, g_{- i}) ≻ \sum_{g \in G} π_{i} (g) u_{i} (g_{i}^{'}, g_{- i})$ , esto puede ocurrir si y sólo si los correspondientes grafos N^i,g y N^i,g’ son tales que:

\hat{ς} (g) < \hat{ς} (g^{'})

Ahora presentamos el corolario que define los hallazgos de esta sección:

Proposición 7: Si se comprueba el SACI y x ≥ 2 entonces el conjunto de redes estrictas de Nash es el conjunto de redes de línea de conexión secuencial con nodos de activación par o impar.

Prueba: (a) Un N_i que no sea una red en línea con nodos de activación par o impar no puede ser equilibrio estricto de Nash. Sea n par.⁴ Esto significa que para al menos un agente i,

\{\begin{matrix} \sum_{g \in G} π_{i} (g) u_{i} (g_{i}, g_{- i}) \neq \sum_{i \in N} I_{i} (n_{i} (g)) - 2, s i i e s a c t i v o o \\ \begin{matrix} \sum_{g \in G} π_{i} (g) u_{i} (g_{i}, g_{- i}) \neq \sum_{i \in N} I_{i} (n_{i} (g)) - 1, s i i e s e l ú l t i m o a g e n t e o \\ \sum_{g \in G} π_{i} (g) u_{i} (g_{i}, g_{- i}) \neq \sum_{i \in N} I_{i} (n_{i} (g)), s i i e s p a s i v o \end{matrix} \end{matrix}

1. Consideremos primero el caso de un agente activo para quien pudiera existir una estrategia de desvío tal que: $\sum_{g \in G} π_{i} (g^{*}) u_{i} (g_{i}^{*}, g_{- i}) > \sum_{i \in N} I_{i} (n_{i} (g)) - 2$ . El acceso a mayor información no puede ser mejorado, dado que actualmente i accede a toda la información disponible en la red y x ³ 2 implica que a partir de la red más pequeña posible (n = 3), i observa toda la red por lo que el equilibrio será entonces conectado (Proposición 4) y mínimo (Proposición 3). i sólo se quedará con aquella topología que otorgue el máximo pago, en primer lugar, y estos pagos sean más igualitarios, en segundo lugar. Volviendo al agente activo, ella evaluará que una estrategia alternativa que depare mayor beneficio sólo debiera considerar la disminución del número de conexiones. Si i optará por conectarse con sólo la agente k + 1 (predecesora) o sólo con k - 1 (antecesora) anularía la conectividad de la red desconectando en dos subredes a la misma. Con ello se accedería a un nivel de información menor que $\sum_{i \in N} I_{i} (n_{i} (g))$ habiéndose ahorrado sólo una unidad de utilidad en costos de conexión. Por otro lado, si i decidiera conectarse con otras agentes ubicadas en k ± j enlaces de distancia, tal que 2 ≤ j ≤ n - j, entonces dejaría aislados a los agentes intermedios k ± k’ con k’ < j. Nuevamente, perdería el acceso a información más valiosa que el beneficio de disminuir los costos de conexión respectivos. Contradicción.

2. Analicemos el caso que i sea el último agente. Si es así, la única manera de desviarse sería cortar su único enlace con el resto de la red. Pero ahorraría una unidad perdiendo toda la información excepto la suya propia. Contradicción.

3. Finalmente, considere ahora el caso de un agente i, tal que i es pasivo. Veamos si existe una estrategia g* tal que $\sum_{g \in G} π_{i} (g^{*}) u_{i} (g_{i}^{*}, g_{- i}) > \sum_{i \in N} I_{i} (n_{i} (g))$ Dado que i accede a toda la información sin incurrir en costo alguno, no hay acción de i que le permita incrementar el beneficio. Contradicción.

(b) Una red desconectada nunca puede ser un equilibrio. Supóngase por contradicción que sí puede ser equilibrio. Entonces debe haber un componente N_i ⸦ N en g* que es una red centralmente sostenida. Sea i el centro de la estrella. Dado que N_i es una estrella, i observa a todos los j ϵ N_i con x = 1. Las creencias de i deben reflejar correctamente quienes integran N_i y quienes no. De acuerdo con esas creencias, i está estrictamente mejor conectándose con todos que quedando aislado. Contradicción.

Entonces, volviendo al ejemplo de cómo construir caminos entre pueblos de una comarca desconociendo el alcance completo de la futura red y con costos acumulativos, el resultado sugiere que cada pueblo (nodo) debiera disminuir dichos costos conectándose con sus vecinos más próximos. Aun desconociendo la ubicación de los otros nodos de expansión de la red este criterio permite extender la red al menor costo posible cuando los costos son acumulativos. Ahora finalizamos el trabajo con las conclusiones.

Conclusiones

La presencia de información imperfecta en un juego formación de red altera el resultado de equilibrio cuando el grado de observación es bajo. Un grado de observación bajo es ineficiente dado que las pérdidas potenciales son mucho mayores bajo este esquema de pagos comparado con el caso de existir un grado de observación mayor. Si el horizonte de observación de enlaces se hace creciente, el resultado óptimo tiende lógicamente al resultado de información perfecta tal cual fue especificado en la Proposición 2. En el caso de que sea posible observar toda la red, resulta óptima al ir conectando los nodos por cercanía, avanzando desde un nodo hacia uno o los dos más cercanos. Es interesante destacar que las redes de información y monitoreo imperfectos son más reales que las redes de Bala y Goyal, por lo que la línea de investigación que une el estudio de las redes sociales y la microeconomía necesariamente pasa por ampliar esta rama de muy reciente creación. En el ejemplo presentado en la introducción, el criterio óptimo para construir las vias romanas sería el de construir hasta un destino específico, luego de allí avanzar con la via al siguiente lugar observable más cercano y así, de modo de no acumular costos.

Como senderos de investigación a futuro, puede citarse i) el análisis de este mismo esquema pero para el caso en el que el flujo de información sea monodireccional; ii) el mismo modelado bajo monitoreo e información imperfecto pero con la presencia de información de diferentes calidades o, en su defecto, información que pierde valor a medida que pasa de agente en agente (flow decay) y, finalmente, iii) podría estudiarse refinamientos o modelizaciones específicos para evitar la ineficiencia por desconexión, alternativos a los presentados por McBride (2006).

Referencias bibliográficas

Bala, Venkatesh y Goyal, Sanjev (2000), “A Noncooperative Model of Network Formation”, Econometrica, 68, pp. 1181-1229, http://www.jstor.org/stable/2999447.

Berninghaus, Siegfried K.; Ott, Marion y Vogt, Bodo (2004), “On networks and ‘stars’ - Recent results in network experiments”, Manuscrito, University of Karlsruhe.

Bondonio, Daniele (1998), “Predictors of accuracy in perceiving informal social networks”, Social Networks, 20, pp. 301-330, doi: https://doi.org/10.1016/S0378-8733(98)00007-0.

Chinowsky, Paul S.; Price, Jason C. y Neumann, James E. (2013), “Assessment of climate change adaptation costs for the U.S. road network”, Global Environmental Change, 23, pp. 764-773, http://dx.doi.org/10.1016/j.gloenvcha.2013.03.004.

Falk, Armin y Kosfeld, Michael (2012), “It’s all about connections: Evidence on network formation”, The Review of Network Economics, 11(3), doi: https://doi.org/10.1515/1446-9022.1402.

Gilli, Mario (1999), “On Non-Nash Equilibria”, Games and Economic Behavior, 27, pp. 184-203, doi https://doi.org/10.1006/game.1998.0664.

Jackson, Michael O. y Zenou, Yves (2015), “Games on Networks”, incluido en H. Peyton Young y Shmuel Zamir (eds.), Handbook of Game Theory with Economic Applications, 4, pp. 95-163, https://doi.org/10.1016/B978-0-444-53766-9.00003-3.

Larrosa, Juan Manuel C. (2005), Ensayos sobre asignación óptima de recursos en redes, tesis doctoral, Departamento de Economía, Universidad Nacional del Sur.

Larrosa, Juan Manuel C. y Tohmé, Fernando (2006). “Redes de equilibrio con costos de conexión acumulativos y comunicación bidireccional”, Estudios Económicos, 42, pp. 67-88, doi: https://doi.org/10.52292/j.estudecon.2005.883.

Laurence, Ray (1998), “Land transport in Roman Italy: costs, practice and the economy”, incluido en Parkins, Helen y Smith, Christopher (eds.), Trade, Traders and the Ancient City, Routledge, Londres.

McBride, Michael (2006), “Imperfect Monitoring in Communication Networks”, Journal of Economic Theory, 126, pp. 97-119, doi https://doi.org/10.1016/j.jet.2004.10.003.

______(2008), “Position-specific Information in Social Networks: Are You Connected?”, Mathematical Social Sciences, 56(2), pp. 283-295, doi https://doi.org/10.1016/j.mathsocsci.2008.05.003.

McBride, Michael y Hewitt, David (2013), “The enemy you can’t see: An investigation of the disruption of dark networks”, Journal of Economic Behavior & Organization, 93, 32-50, doi https://doi.org/10.1016/j.jebo.2013.07.004.

Nava, Francesco y Piccione, Michele (2014), “Efficiency in repeated games with local interaction and uncertain local monitoring”, Theoretical Economics, 9(1), pp. 279-312, doi: 10.3982/TE1200.

Shipley, Frederick (1931), “Chronology of the Building Operations in Rome from the Death of Caesar to the Death of Augustus”, Memoirs of the American Academy in Rome, 9, pp. 7-60, http://www.jstor.org/stable/4238552.

Notes

[1] Jackson y Zenou (2015) representan una introducción recomendada para los interesados en la temática de redes y juegos no cooperativos.

[2] Con este supuesto descartamos la posibilidad de la aparición de la red vacía (es decir, los agentes permanecen todos aislados) como estructura de equilibrio en nuestro modelo.

[3] Con este supuesto descartamos la posibilidad de la aparición de la red vacía (es decir, los agentes permanecen todos aislados) como estructura de equilibrio en nuestro modelo. Supongamos el ejemplo del camino entre pueblos como vector de comunicaciones presentado en la introducción: ello representaría algo valioso por lo que un nodo puede evaluar para conectarse a la red.

[4] Para la demostración no importa necesariamente si es una red de nodos activos pares o impares dado que con modificaciones triviales se obtiene el mismo resultado. Lo mismo ocurre en considerar n par o impar.